
2019-05-18
早起,满世界都是关于老贝的话题,转载图片一波一波的,都是曾经见过的,故事讲了一遍又一遍也都是听过的,一个感觉,就是全体附庸风雅的低级波。
几何和架构是两个基本相关的学科。最公认的几何形状之一是三角形。三角形由三个角度识别,这三个角度通过线段连接以形成三边形状,建筑中使用的两种最常见的三角形形式是等边和等腰。
三角形是建筑的有效工具,用于建筑物和其他结构的设计,因为它们提供强度和稳定性。当建筑材料用于形成三角形时,设计具有沉重的底部,并且顶部的顶峰能够处理重量,因为能量如何在整个三角形中分布。这就是为什么许多住宅有A型框架的原因; 它提供了坚固的结构。三角形中最坚固的是等边和等腰; 它们的对称性有助于分配重量。
等边三角形是迄今为止建筑中最常用的三角形。等边三角形具有三个全等边和每个角上60度的角度。两侧的长度各不相同。建筑中使用的等边三角形的一个常见例子是埃及的吉萨金字塔复合体。形成金字塔的四个三角形边中的每一个都是等边三角形。这些是建筑中三角形强度的例子,因为金字塔已经存在了4000多年。
等腰三角形有两个相等的边,在世界各地的建筑中也有发现,特别是在现代金字塔结构中。在华盛顿特区国家美术馆的东楼建筑中使用了等腰三角形。该建筑由着名建筑师贝聿铭设计。他的建筑风格以等腰三角形和其他几何形状为特色。大楼被建造在一块形状奇特的三角形地块上。贝聿铭使用等腰三角形作为建筑物的基础,以适应情节的形状,这个建筑成了他的经典之作。
斜角三角形是所有边都不一致的三角形。不等边三角形三角形在建筑中不常见。这些三角形中没有对称性,导致重量分布不均匀。这是危险的,因为一个角度将比另一个角度具有更多的重量和压力。直角三角形有一个完美的90度角。这些特殊三角形传统上不用于建筑物的结构特征。然而,它们对建筑物的建造和设计至关重要。直角三角形用于创建完美的角落和直线。如果建筑物的墙壁和角落弯曲,建筑物也会弯曲。
构成世间万物的最小单元就是四面体,把四面体拆开就是四个三角形。也就是说三个三角形相加等于四个三角形,而这是个三角形构成一个稳定的四面体,其数学公式是:1+2=4。记得我在2007年写过一篇博文,说的就是这个。
1+2=4(转自自己的新浪博客2007-06-15 02:11:50)
看上去这是个奇怪的等式。
当看了下面的图呢也许就打消了这个念头,但前提必须是读懂这个图真正意义。它不是简单的验证等式的成立与否,关键是在说明这个四是个“四面体”,它是构成世界万物的最小单元。
这里的“1”不是简单的数字概念,它是一个三角形的量的表示。1个三角形+2个三角形=4个三角形。
这是美国科学家、建筑艺术家、哲学家、发明家、诗人福勒的研究发明.
两个四面体构成一个六面体,以此类推下去,正方体,球体等等千变万化的形体就像着了魔似的繁衍开来。
最常见的球节点便是使用最广的建筑结构形式。

关于四面体说来话长,那是1988年,恩师柳冠中老师给我们上课,让我们做一个标准的单元体构成一个稳定的结构。几天都没感觉,班上的其他同学也都是丈二和尚摸不着头脑,后来去手工车间看见一个ABS塑料片,于是就用塑料条做了一个三 (leng)锥,三 (leng)锥的六根条都是完全一样的条的两端也是完全相同的结构,三根条一个结构点相互拧着卡住。作业就是这样完成了,当时也不知道是对还是不对,当时就没有四面体的概念更不知道富勒是谁。交了作业柳老师当时也没说什么,但是给了一个很高的分数着实不解。

四面体

六面体

八面体




1989年去日本留学,看的第一个展览就是富勒的,顿时恍然大悟,原来我做的那个三(leng)锥就是四面体……而且是构成万物的最小单元,对于几何结构的理解从那一刻算是才明白,在后来的设计中已经习惯了用这种方式思考问题解决问题,也设计了很多构成类的作品。
想起2017年验算过关于金字塔的比例与原理,那时贝律铭正好是100岁,很巧合的是,用19个单元叠加每层减掉2两个单元,到顶端正好是100个单元。如果每个单元的比例是正方形的话,这100个单元组合的三角形正好是等腰三角形,将其拷贝旋转就是一个正方形。如果将这个关系做成立体四棱锥的话,那么每个立面上的单元也必然是100个单元。

二维等腰三角塔
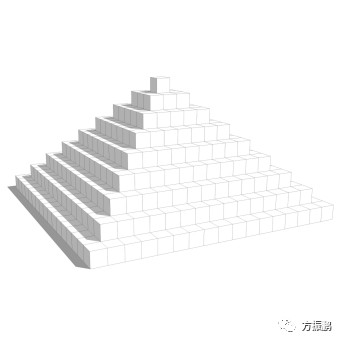
三维等腰三角塔(类似坛城塔)

俯视三角塔与45度角度的影子

去掉单元格所呈现的还是等腰三角形
贝聿铭的建筑当中最喜欢用的就是三角形和几何形,他沉迷于对几何精确度的偏爱,不管怎样这种具有神圣几何原理的方式是解释万物构成的最小单元——四面体的载体,所以他的建筑设计都是以锐利的直线,单纯的构造,会让你感觉到结构的透明性,这恰恰是对几何性魅力最直接的解释。贝律铭的建筑从某种意义上讲,是不是可以理解为遵循神的旨意呢?或者说是立体主义呢?这个神应该指的是自然规律和自然原本的信息。

卢浮宫金字塔(图片来自网络)

由埃及金字塔而来的三角塔原理

将三角塔与贝聿铭的金字塔巧妙地重合

等腰三角塔的投影后的等腰三角形

投影后的等腰三角形与卢浮宫金字塔的巧妙重合
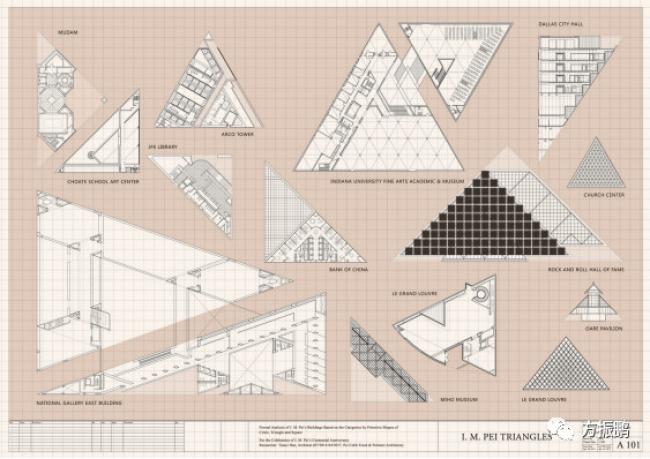
等腰三角塔与贝聿铭设计图纸的重合
伊斯兰艺术博物馆
贝聿铭曾经说过,标签是一个陷阱。“我不羡慕那些拥有如此强烈的风格印记的建筑师,如果他们的项目没有得到同样的'外观',客户会感到失望......我认为我有更大的自由。”他在伊斯兰艺术博物馆训练了这种自由,这是一个白色的海市蜃楼,就像一个从波斯湾水域涌入多哈硬眩光的糖块宫殿。就像Candide寻找幸福一样,贝聿铭去寻找伊斯兰建筑的“本质”。他拒绝了科尔多瓦的大清真寺,大马士革的倭马亚清真寺和突尼斯的里巴特堡垒,最终在开罗的艾哈迈德伊本图伦清真寺的宁静中找到了他所寻找的东西。在那里,一个大型拱形法院的方形房间上的圆形圆顶表达了几十年来在他脑海中跳舞的嵌套几何形状。在他最终设计的博物馆中,伊斯兰建筑最纯粹的升华也证明了他在20世纪40年代作为学生吸收的Beaux-Arts多边形和严厉的现代主义正统的完美结合; 他所召唤的所有坚实的,岩石般的存在和轻快的中庭。贝聿铭在异国情调的土地上进行了探索,终于找到了他自己。








以上图片均来自网络
香港中国银行
贝聿铭为香港中国银行设计了一座摩天大楼,其繁华的不对称性使香港的天际线成为焦点。看上去非对称的外表,其实是由稳定的等腰三角形构成的。这是来自他的修炼和品味,以及他对建筑的救赎力量的信念。
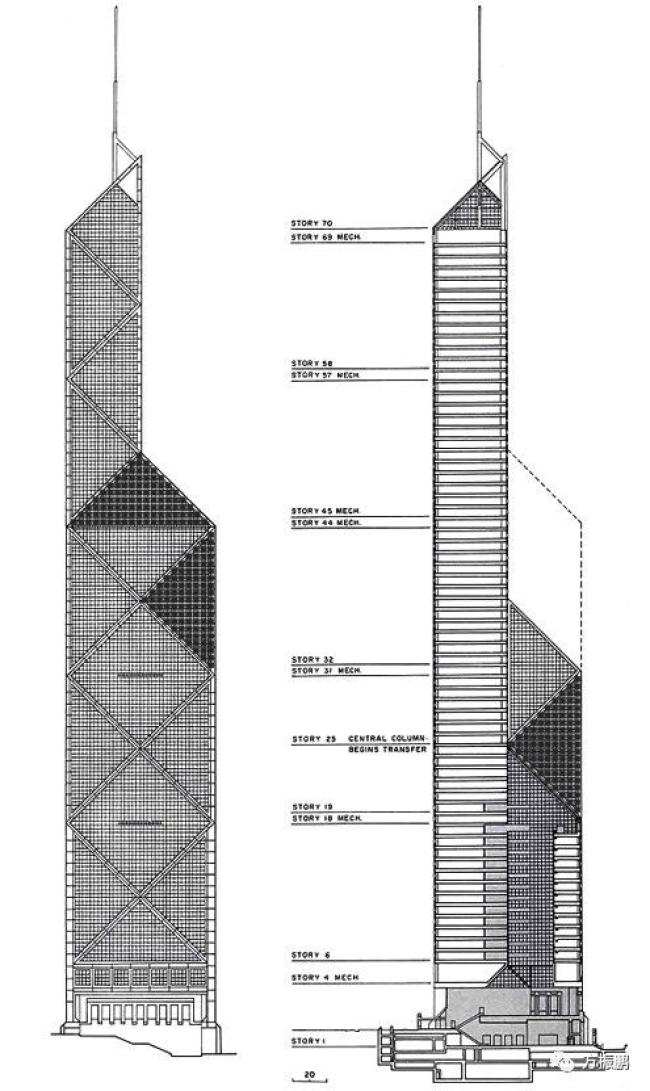
华盛顿特区国家美术馆的东楼
在华盛顿特区国家美术馆的东楼建筑中使用了等腰三角形。该建筑由着名建筑师贝聿铭设计。他的建筑风格以等腰三角形和其他几何形状为特色。大楼被建造在一块形状奇特的三角形地块上。贝聿铭使用等腰三角形作为建筑物的基础,以适应情节的形状,这个建筑成了他的经典之作。









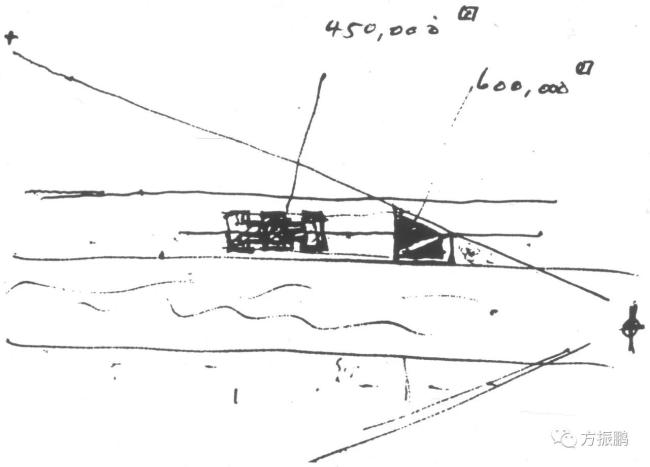


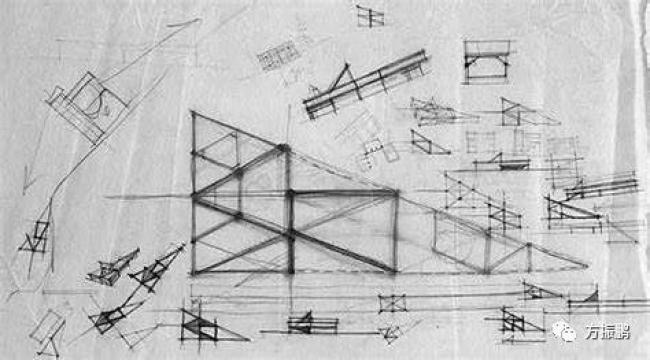

以上图片均来自网络
几何学的神秘
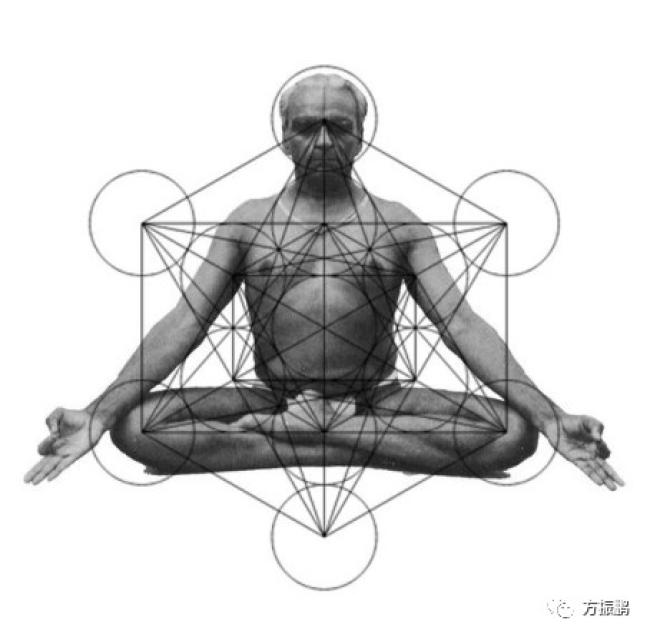
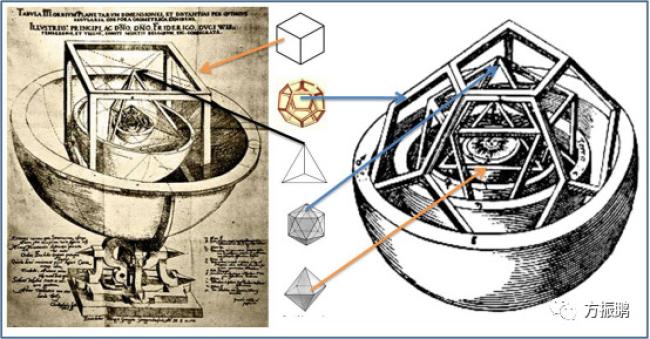
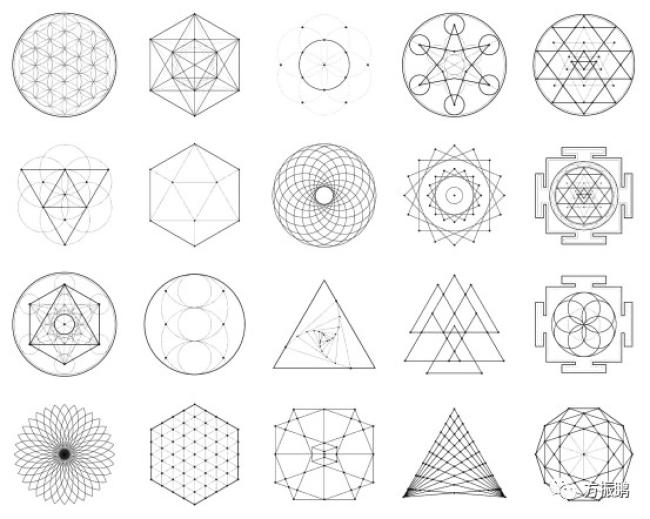
神圣的几何形状赋予某些几何形状和某些几何比例的符号和神圣含义。它与认为神是世界的几何学的信念有关。用于设计和建造宗教结构的几何学,如教堂,寺庙,清真寺,宗教纪念碑,祭坛和住棚节,有时被认为是神圣的。这个概念也适用于神圣的空间,如temenoi,神圣的小树林,村庄的绿地和圣井,以及宗教艺术的创造。
根据几何计划,神创造宇宙的信念具有古老的起源。普鲁塔克将这种信仰归功于柏拉图,写下“柏拉图说上帝不断地进行几何化”。在现代,数学家卡尔弗里德里希高斯改编了这句话,称“上帝算术”。直到约翰尼斯开普勒(1571-1630),一些科学家对宇宙的几何基础的信念仍然存在。

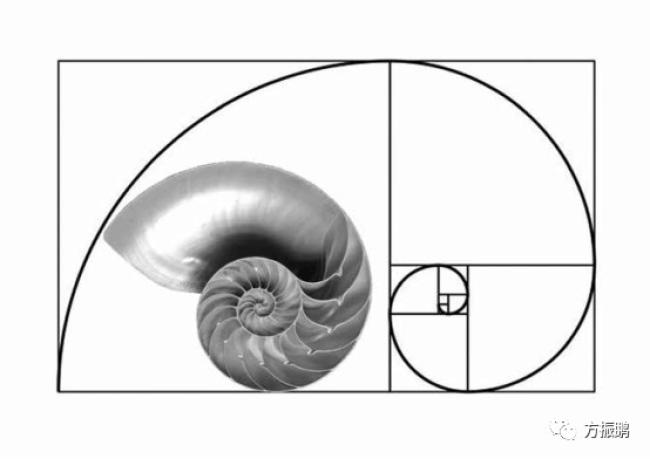
据斯蒂芬·斯金纳,神圣的几何的研究在对自然的研究它的根源,以及数学原理工作在其中。在自然界观察到的许多形式都与几何有关; 例如,有腔的鹦鹉螺以恒定的速率生长,因此它的外壳形成一个对数螺旋,以适应这种增长而不改变形状。此外,蜜蜂构建六角形细胞以容纳它们的蜂蜜。这些和其他对应关系有时根据神圣的几何形状来解释,并被认为是几何形式的自然意义的进一步证明。
几何比例和几何图形经常用于古埃及,古印度,希腊和罗马建筑的设计中。中世纪的欧洲大教堂也采用了符号几何。印度和喜马拉雅的精神社区经常在曼陀罗和扬特拉的设计计划上建造寺庙和防御工事。
人体和古代建筑的许多神圣几何原理被编入莱昂纳多达芬奇的维特鲁威人绘画中。后者的绘画本身是基于罗马建筑师维特鲁威的古老着作。
伊斯兰的几何图案也是众所周知的,它们在古兰经,清真寺以及个人名字的书法中使用。
该Agamas是梵语的集合,泰米尔语和Grantha 译经主要构成寺庙建筑和偶像的创作,神灵崇拜的手段,哲学学说,冥想练习,六倍欲望的实现,并4种方法瑜伽
在Agamas for Shilpa(雕塑艺术)中制定了精心制定的规则,描述了诸如建造寺庙的地方,要安装的图像种类,制作它们的材料等物质的质量要求。它们的尺寸、比例、空气流通和寺庙建筑群的照明等等。该Manasara和Silpasara是这些规则处理工程。寺庙每日礼拜的仪式也遵循阿加玛斯规定的规则。
中世纪欧洲大教堂的建造通常基于几何形状,旨在使观众通过数学看世界,并通过这种理解,更好地理解神圣。这些教堂经常采用拉丁十字架平面图,其原因就是遵循自然法则的定律和几何美学。
在欧洲文艺复兴初期,观点转向了简单和规则的几何形状。特别是圆形成为建筑基础的中心和象征形状,因为它代表了自然的完美和人类在宇宙中的地位的中心地位。在莱昂巴蒂斯塔-阿尔贝蒂的建筑论文中,圆形和其他简单对称几何形状的使用被固化为文艺复兴时期宗教建筑的主要内容,其中描述了理想教会在精神几何方面的作用。
